30、终章：阿姆达尔定律（Amdahl‘s Law）

阿姆达尔定律可用于推测计算量通过部分并行运行可以加速多少。阿姆达尔定律以吉恩·阿姆达尔（Gene Amdahl）的名字命名，他在1967年提出了该定律。即使不知道阿姆达尔定律，大多数使用并行或并发系统工作的开发人员都对潜在的加速有着直觉的感觉。无论如何，了解阿姆达尔定律可能仍然有用。

我将先以数学方式解释阿姆达尔定律，然后使用图表说明阿姆达尔定律。

阿姆达尔定律定义

可并行化的程序（或算法）可以分为两部分：

无法并行化的部分
可以并行化的部分

设想一个处理磁盘文件的程序。该程序的一小部分可能会扫描目录并在内存内部创建文件列表。之后，每个文件都传递到单独的线程进行处理。扫描目录并创建文件列表的部分无法并行化，但处理文件可以并行化。

串行（非并行）执行程序所花费的总时间称为T。时间T包括不可并行部分和可并行部分的时间。不可并行化的部分称为B。可并行化的部分称为T-B。以下列表总结了这些定义：

T = 串行执行总时间
B = 不可并行化部分的总时间
T - B = 可并行化部分的总时间（串行执行时，而非并行时）
由此可见：

T = B + (T-B)

乍一看，程序的可并行化部分在方程式中没有自己的符号，可能看起来有些奇怪。但是，由于可以使用总时间T和B（不可并行化的部分）表示方程的可并行化部分，因此实际上从概念上简化了方程，这意味着该形式包含的变量较少。

可以通过并行执行而加速的部分是可并行化部分T-B。可以加速多少取决于申请了多少个线程或CPU来执行。线程或CPU的数量称为N。因此，可并行化部分可以执行的最快速度是：

(T - B) / N

另一种写法是：

(1/N) * (T - B)

根据阿姆达尔定律，使用N个线程或CPU执行可并行化部分时，程序的总执行时间为：

T(N) = B + (T - B) / N

T（N）表示并行度为N的全部执行时间。因此，T可以写为T（1），并行度为1的总执行时间。使用T（1）代替T，阿姆达尔定律看起来像像这样：

T(N) = B + ( T(1) - B ) / N

其含义是一样的。

一个推算示例

为了更好地理解阿姆达尔定律，我们来看一个推算示例。执行程序的总时间设置为1。程序的不可并行化部分为40％，所以1的40%等于0.4。因此，可并行化部分等于1-0.4 = 0.6。

并行度为2（可并行化部分由2个线程或CPU执行，因此N为2）的程序的执行时间将为：

T(2) = 0.4 + ( 1 - 0.4 ) / 2
     = 0.4 + 0.6 / 2
     = 0.4 + 0.3
     = 0.7

若并行化系数使用5而不是2，进行相同的计算将如下所示：

T(5) = 0.4 + ( 1 - 0.4 ) / 5
     = 0.4 + 0.6 / 5
     = 0.4 + 0.12
     = 0.52

图解阿姆达尔定律

为了更好地理解阿姆达尔定律，我将尝试说明该定律是如何得出的。

首先，程序可分解为不可并行化的部分B和可并行化的部分1-B，如下图所示：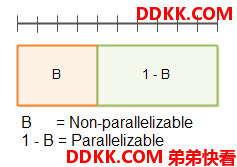

顶部带有分隔符的行是总时间T（1）。
下面是并行度为2的执行时间：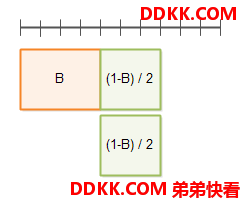

下面是并行度为3的执行时间：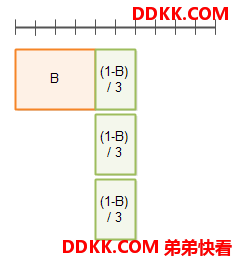

优化算法

根据阿姆达尔定律，可以很自然的推论出，可并行化部分可以通过堆硬件来加速执行。即使用更多线程或 CPU。但是，不可并行化的部分只能通过优化代码来加速执行。因此，可以通过优化不可并行化的部分来提高程序的速度和并行性。通常，你甚至可以通过将一些工作移到可并行化部分中（如果可行），来将算法更改为具有较小的不可并行化部分。

优化串行部分

如果要优化程序的串行部分，还可以使用阿姆达尔定律来计算优化后程序的执行时间。如果将不可并行部分B以因数O来优化，则阿姆达尔定律表示为：

T(O,N) = B / O + (1 - B / O) / N

请记住，程序的不可并行化部分现在需要B / O时间，因此并行化部分需要1-B / O时间。

如果B为0.4，O为2，N为5，则计算如下：

T(2,5) = 0.4 / 2 + (1 - 0.4 / 2) / 5
       = 0.2 + (1 - 0.4 / 2) / 5
       = 0.2 + (1 - 0.2) / 5
       = 0.2 + 0.8 / 5
       = 0.2 + 0.16
       = 0.36

执行时间与加速

到目前为止，我们仅使用阿姆达尔定律来计算优化或并行化后程序或算法的执行时间。我们还可以使用阿姆达尔定律计算加速比，也就是新算法或程序比旧版本快多少。

如果程序或算法的旧版本时间为T，则加速比为

Speedup = T / T(O,N)

我们通常将T设置为1，只是为了计算执行时间和加速时间是原来的几分之一。等式如下所示：

Speedup = 1 / T(O,N)

如果我们用阿姆达尔定律计算公式替换T（O，N），则会得到以下公式：

Speedup = 1 / ( B / O + (1 - B / O) / N )

在B= 0.4，O = 2和N = 5的情况下，计算公式为：

Speedup = 1 / ( 0.4 / 2 + (1 - 0.4 / 2) / 5)
        = 1 / ( 0.2 + (1 - 0.4 / 2) / 5)
        = 1 / ( 0.2 + (1 - 0.2) / 5 )
        = 1 / ( 0.2 + 0.8 / 5 )
        = 1 / ( 0.2 + 0.16 )
        = 1 / 0.36
        = 2.77777 ...

这就是说，如果以因数2来优化不可并行化（串行）部分，并以因数5并行执行可并行化部分，则该程序或算法优化后的新版本的运行速度最多比旧版本快2.77777倍。

要测量，别仅是计算

尽管阿姆达尔定律使你能够计算算法并行化的理论速度，但不要过分依赖此类计算。实际上，在优化或并行化算法时，也可能受许多其他因素影响。

内存，CPU高速缓存，磁盘，网卡等（如果使用磁盘或网络）的速度也可能是限制因素。如果新版本算法在并行化时，导致更多的CPU高速缓存未命中，你可能无法获得想要的使用 N个CPU带来xN的加速。如果新版本算法最终使内存总线，磁盘，网卡或网络连接饱和，情况也是如此。

我的建议是使用阿姆达尔定律来了解在何处进行优化，但要使用度量方法来确定优化的实际加速。请记住，有时，高度序列化的串行（单CPU）算法可能会优于并行算法，这仅仅是因为串行算法没有协调开销（分解工作并重新聚合），而且因为单个CPU算法可能更好地符合底层硬件的工作方式（CPU管道，CPU缓存等）。